Clustering Crash Simulation Data with LLCA

In this article, I will present a summary of the results of a guided research project (TUM module, KTH module) which I have worked on in cooperation with both SCCS (Chair of Scientific Computing) at Technische Universität München (TUM), and CVAP (Computer Vision and Active Perception Lab) at Royal Institute of Technology, Stockholm (KTH). The full report is also available.

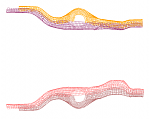
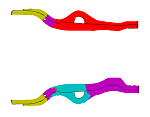
The problem is as follows: The finite element model of a car and a series of car crash simulations with different parameters are given. The task is to cluster the finite element nodes such that nodes within a cluster are similarly displaced in the crash simulations. The bigger picture is given in a paper by Bohn et al. [1]. For now, we have looked only onto four chassis beams as highlighted in the following figure.

The idea for solving this task is based on a paper by Wu and Schölkopf [2] who present the local learning based clustering algorithm (LLCA). This clustering method looks for a labeling where the label for each data point can be well-predicted by a local classifier trained on the labels of neighboring data points. The cost function of the clustering method is hence based on local classifiers.

Like the authors of the original method, I used kernel ridge regression for the local classification task. However, the model of the four chassis beams alone comprises over 6000 finite element nodes. In order to make the method tractable, I picked up the idea of my supervisor to implement an out-of-sample extension that is based on a support vector machine. Only a part of the data is clustered by LLCA. The resulting labeling is used to train a support vector machine which in turn will assign labels to the whole dataset.

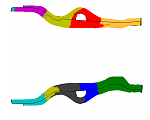
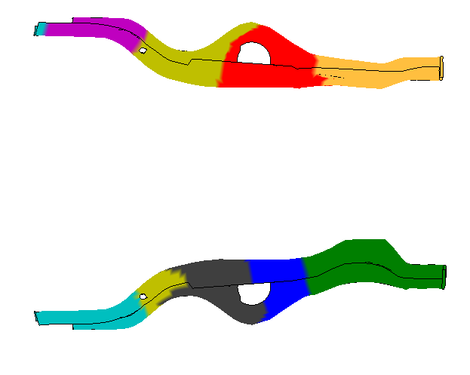
The results are not so easy to interpret. The clusterings of the chassis beams look somehow similar as in the paper by Bohn et al. [2] who employ both k-means and sparse-grid based spectral clustering instead. The following figure shows the clustering obtained with our LLCA variant.

This research work required the combination of several algorithms. I believe that research should be reproducible, especially in areas such as computer science where the necessary hardware for reproducing results is comparably easy to obtain. A small step in this direction is that a C++ implementation of LLCA with the optional SVM-based out-of-sample extension is open source.

References

[1] B. Bohn, J. Garcke, R. Iza-Teran, A. Paprotny, B. Peherstorfer, U. Schepsmeier, and C.-A. Thole, “Analysis of Car Crash Simulation Data with Nonlinear Machine Learning Methods,” in International Conference on Computational Science, 2013.

[2] M. Wu and B. Schölkopf, “A Local Learning Approach for Clustering,” in Advances in Neural Information Processing Systems, 2006.