13. Mai 2011

Sampling from a Poisson distribution - a benchmark

Having a poisson-distributed random variable X, how can we efficiently generate samples (or say realizations) of that random variable? This article shows how Knuth’s technique can be derived and it also indicates that the Ratio-of-Uniforms method is quite efficient.

X is the number of arrivals in a poisson process within a fixed period of time. The inter-arrival times follow an exponential distribution. The following small benchmark makes an attempt to compare the time necessary to compute samples using three different algorithms:

  1. Algorithm exp, do it yourself
  2. Algorithm uni by D. Knuth
  3. Algorithm rou, from Numerical Recipes

(Let’s peek at the results up-front: rou seems to win this challenge!)

exp – counting inter-arrival times

We want a random sample of the number of arrivals within a fixed period of time. We know the distribution of the inter-arrival times. By summing up inter-arrival times until the sum exceeds the fixed period of time (use the unit interval for convenience) we generate a sample number of arrivals. Formalizing this idea, we have a sequence of exponentially distributed random values:

$$T_1, T_2, T_3 \dots \qquad \sim \qquad Exp(\lambda)$$

The i-th interval represents the time until the i-th arrival. We then find a number k such that

$$\sum_{i=1}^k T_i \le 1 \le \sum_{i=1}^{k+1} T_i $$

This number k is the sought-after random sample.

double exponential(Ran *ran, double lambda) {
    double p;
    do {
        p = ran->doub();
    } while (p == 0.);
    return -log(p) / lambda;
}

int poisson_exp(Ran *ran, double lambda) {
    double t = 0;
    int k = 0;
    while (1) {
        t += exponential(ran, lambda);
        if (t > 1) {
            return k;
        } else {
            k++;
        }
    }
}

uni – counting inter-arrival times, improved

Usually, the inversion method is used for sampling from an exponential distribution.

$$U_1, U_2, U_3 \dots \qquad \sim \qquad Uniform(0, 1)$$ then $$T_i = - \frac{1}{\lambda} \ln U_i \qquad \sim \qquad Exp(\lambda) $$

Note the logarithm. It is the computationally most expensive operation when generating a sample inter-arrival time. Knuth’s variant gets rid of this nuisance. Here’s how it works

$$ \begin{aligned} \sum_{i=1}^k T_i &\le 1 \le \sum_{i=1}^{k+1} T_i \\ \sum_{i=1}^k \left( - \frac{1}{\lambda} \right) \ln U_i &\le 1 \le \sum_{i=1}^{k+1} \left( - \frac{1}{\lambda} \right) \ln U_i \\ \sum_{i=1}^{k+1} \ln U_i &\le - \lambda \le \sum_{i=1}^{k} \ln U_i \\ \ln \prod_{i=1}^{k+1} U_i &\le - \lambda \le \ln \prod_{i=1}^{k} U_i \\ \prod_{i=1}^{k+1} U_i &\le \exp(-\lambda) \le \prod_{i=1}^{k} U_i \end{aligned} $$

Finding a k that satisfies the last inequation only requires λ+1 uniform samples on average, reflecting in shortened computation times. 

int poisson_uni(Ran *ran, double lambda) {
    int k = -1;
    double p = 1.;
    double lambda_exp = exp(-lambda);
    do {
        k++;
        p *= ran->doub();
    } while (p > lambda_exp);
    return k;
}

rou – using Ratio-of-Uniforms method

No explanation here (unfortunately…). Just take the algorithm from Numerical Recipes and see what it’s worth. Actually, I modified it to use Ratio-of-Uniforms for all values of λ for the sake of comparison. Sources are licensed and therefore cannot be listed here.

Benchmark

Taking different values for λ (1, 2, 4, 16, 32, 64) and generating a million random samples using each of the three algorithms on a notebook from 2008, here’s the results (interpolated).

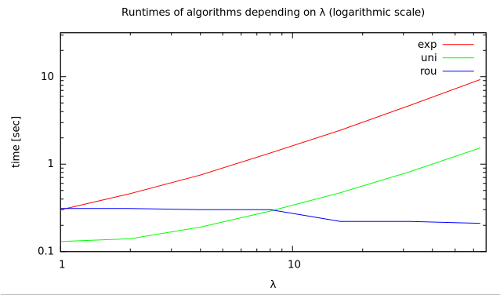
 g++ -O2 benchmark.cpp -I . -o benchmark
./benchmark
 Numbers generated per algorithm: 1000000
Expected value: 1
    method       mean   time [s]
       uni      1.000      0.130
       exp      0.998      0.300
       rou      1.036      0.310
 Numbers generated per algorithm: 1000000
Expected value: 2
    method       mean   time [s]
       uni      2.001      0.140
       exp      2.000      0.460
       rou      2.008      0.310
 Numbers generated per algorithm: 1000000
Expected value: 4
    method       mean   time [s]
       uni      3.999      0.190
       exp      3.999      0.750
       rou      4.000      0.300
 Numbers generated per algorithm: 1000000
Expected value: 8
    method       mean   time [s]
       uni      8.000      0.290
       exp      8.000      1.340
       rou      8.001      0.300
 Numbers generated per algorithm: 1000000
Expected value: 16
    method       mean   time [s]
       uni     16.002      0.470
       exp     15.996      2.440
       rou     16.000      0.220
 Numbers generated per algorithm: 1000000
Expected value: 32
    method       mean   time [s]
       uni     32.007      0.820
       exp     32.001      4.710
       rou     31.996      0.220
 Numbers generated per algorithm: 1000000
Expected value: 64
    method       mean   time [s]
       uni     63.982      1.530
       exp     64.009      9.270
       rou     63.995      0.210

Sources

benchmark.zip : In order to compile, you need to obtain files nr3.h, ran.h, deviates.h, gamma.h from Numerical Recipes and put them into the folder with the other source files.